Temperatura de flexión por calor: retos del análisis mecánico dinámico
La presentación de los datos del DMA a veces puede frustrar a los usuarios y desalentar su adopción. Aquellos que no estén familiarizados con el DMA deben insistir en recibir datos relevantes a la forma en que se utilizará la pieza que están desarrollando.
#tpe
Nota del editor: Esta es la primera parte de un especial con cuatro entregas. Puede encontrar las ligas de la serie completa a continuación:
Parte 1: propiedades de los plásticos.
Parte 3: por qué es mejor la curva DMA.
Parte 4: retos del análisis mecánico dinámico para medir propiedades de materiales.
Después de haber recomendado con frecuencia que los ingenieros que diseñan nuevos productos accedan a los datos DMA, es desalentador cuando regresan algo desconcertados por lo que obtienen de un proveedor de materiales o una base de datos de terceros. A menudo hay problemas con la forma en que se presentan los datos, y es necesario algunas investigaciones antes de que el valor completo de los datos se haga evidente.
Para explicar esto completamente, es mejor comenzar con una ilustración del alcance completo del resultado de un escaneo de temperatura del DMA. Esto se muestra en la Fig. 1 y representa los resultados de un nylon 6 reforzado con fibra de vidrio. Se trazan tres propiedades. La más accesible de estas a alguien familiarizado con las propiedades del material es el módulo de almacenamiento, conocido más formalmente como el módulo elástico.
Este a menudo se confunde con el módulo de Young porque otra designación para el módulo de Young es módulo de elasticidad. Pero el módulo de Young es una medida de rigidez calculada midiendo el cambio en la longitud de una muestra cuando se coloca bajo una tensión uniaxial, ya sea en tensión o compresión. Este concepto se desarrolló mucho antes de que se conocieran los polímeros y se utilizó para caracterizar las propiedades de los metales, donde la relación entre tensión y alargamiento es lineal para una parte significativa de la curva de tensión-alargamiento.
Mientras que el módulo de Young puede ser una descripción útil para metales y otros materiales que presentan principalmente un comportamiento lineal bajo tensión, los plásticos son notoriamente no lineales una vez que se supera un alargamiento de 0.25-0.5%. E incluso en la llamada zona lineal, aspectos no lineales del comportamiento material están presentes, aunque pueden estar ocultos.
Se supone que la deformación dentro de la región elástica es completamente recuperable. Pero en los plásticos, incluso si la tensión se mantiene dentro del rango lineal, se observará un aumento del alargamiento conocida como fluencia o flujo frío si la tensión se mantiene durante un período de tiempo suficiente. La fluencia es esencialmente una velocidad muy lenta de flujo viscoso y es esta respuesta viscosa la que produce la no linealidad.
Fundamentalmente, los plásticos son viscoelásticos; se comportan como una mezcla de un sólido elástico y un fluido viscoso. El aspecto elástico proporciona resistencia, rigidez y la capacidad de un material para recuperarse de una tensión aplicada que deforma el material.
El aspecto viscoso nos da propiedades como la ductilidad y la amortiguación a vibraciones. Para entender realmente el comportamiento de un material, es necesario cuantificar la contribución de ambos tipos de comportamiento. El DMA logra esto separando el módulo que tradicionalmente medimos en sus componentes elásticos y viscosos. El módulo que comienza justo por encima de 800 ksi cerca de la temperatura ambiente representa ese componente elástico.
El aspecto viscoso del comportamiento del material es capturado por la curva etiquetada como el módulo de pérdida, conocido más formalmente como el módulo viscoso. La tercera curva, designada como tan delta, es la relación del módulo viscoso dividido por el módulo elástico.
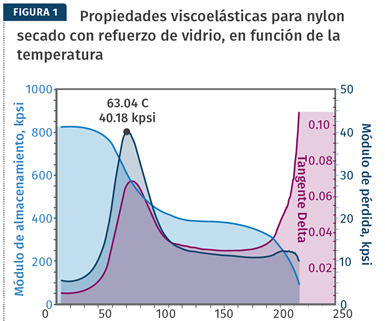
Un examen de la gráfica en la fig. 1 muestra que estas tres propiedades cubren rangos muy diferentes. El módulo elástico varía de unos 100 a 800 ksi y se escala de 0 a 1000 ksi. El módulo viscoso oscila entre los valores de aproximadamente 5 a 40 ksi y se escala de 0 a 50 ksi. La curva tan delta apenas se eleva por encima de 0.10. Uno de los mayores problemas con la presentación de estos resultados es que los editores a veces utilizan una escala para las tres propiedades. Esto es adecuado para presentar el módulo elástico, pero las otras dos propiedades aparecen como líneas planas desprovistas de cualquier característica distintiva, como los picos asociados con la temperatura de transición vítrea.
Un segundo problema es la tendencia a trazar los datos en una escala logarítmica en lugar de una escala lineal. Este sesgo proviene del tratamiento histórico del DMA como una herramienta de investigación y desarrollo utilizada principalmente por los profesionales que se sienten cómodos con las gráficas logarítmicas.
Hay ocasiones en las que las presentaciones logarítmicas son útiles, como con las curvas de viscosidad frente a las curvas de velocidad de cizallamiento. Y si se debe capturar un cambio en particular que abarca varios órdenes de magnitud, una presentación logarítmica da una claridad muy necesaria. Pero en la mayoría de los casos, al menos con materiales semirrígidos y rígidos, las gráficas logarítmicas no añaden tal claridad, hacen que sea más difícil localizar un valor específico en la curva y con frecuencia reducen el impacto visual de una transición significativa en las propiedades.
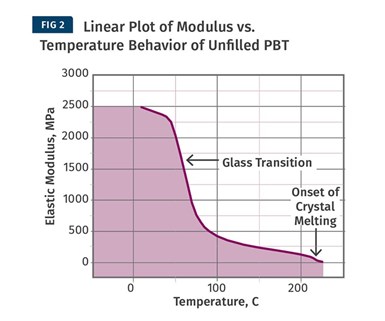
Desempeño lineal de módulo vs. comportamiento de la temperatura de PBT sin relleno.
La figura 2 muestra la gráfica lineal del módulo elástico para el poliéster PBT sin relleno que se analizó en la parte 2 de esta serie, pero se ha ampliado a 25 C para mostrar el comportamiento del material a medida que se acerca al punto de fusión del polímero. Esta adición apenas se nota cuando se traza de esta manera porque para cuando el material alcanza este rango de temperatura, ha perdido más del 95% de su rigidez a temperatura ambiente y las últimas etapas que conducen a la fusión de cristales juegan un papel menor en el gran esquema de las cosas.
La figura 3 proporciona los mismos datos con el módulo trazado en una escala logarítmica. Con esta presentación, el proceso de fusión toma protagonismo y la transición vítrea, que implica un cambio muy grande en el módulo que causó tantos dolores de cabeza a mi cliente citado en la parte 2 de esta serie, es apenas perceptible. Parece algo intrascendente debido al incremento.
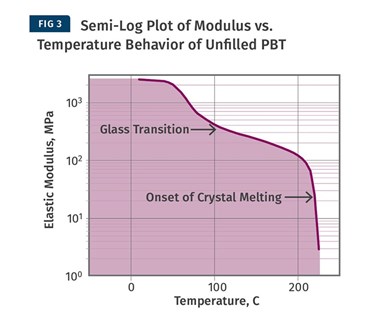
Temperatura de flexión por calor vs. análisis mecánico dinámico.
Un tercer problema implica el tipo de módulo que se mide. El módulo elástico que se traza en las figuras 2 y 3 se conoce como E’ (o módulo de almacenamiento de tracción) y a temperatura ambiente está de acuerdo con los valores de la hoja de datos para el módulo de tracción o el módulo de flexión. Un instrumento DMA debidamente calibrado operado en el modo apropiado debe proporcionar un valor para E’ - que está de acuerdo estrechamente con el valor que se obtendría para un módulo medido en tensión o en flexión. Pero con frecuencia, el valor proporcionado por el DMA en las bases de datos es el módulo elástico en la cizalla, designado como G.
Esto se debe al hecho de que los primeros instrumentos de DMA funcionaban en torsión y, por lo tanto, el módulo de cizallamiento era la propiedad que se estaba midiendo. De hecho, en los primeros días del DMA la técnica se conocía como análisis de trenza torsional (TBA) y las gráficas se daban rutinariamente en G’, G” y tan delta, todos ellos trazados logarítmicamente.
Pero en la mayoría de las aplicaciones, los valores de módulo de tracción son más adecuados para describir los casos de carga asociados a una aplicación. El módulo de tracción y el módulo de cizallamiento están relacionados por una ecuación relativamente simple donde la única otra variable es la relación de Poisson.
Para la mayoría de los polímeros y elastómeros, la relación de Poisson cae entre 0.3 y 0.45, por lo que el valor del módulo de cizallamiento será aproximadamente 35-40% del valor del módulo de tracción. Por lo tanto, un ingeniero que no esté familiarizado con las complejidades de la instrumentación y la convención del DMA recibirá un gráfico que subestima significativamente la rigidez real del material que se está evaluando. Por ejemplo, el PBT sin relleno que hemos estado discutiendo tendrá un módulo de cizallamiento elástico de sólo 875 MPa (127 kpsi), frente al módulo de tracción elástico de 2415 MPa (350 kpsi).
Si bien todos estos obstáculos son molestias relativamente menores, desalientan la adopción de un enfoque muy superior para evaluar las propiedades del material en función a la temperatura.
Se necesita tiempo para acostumbrarse a una nueva forma de hacer las cosas, y cuando ese nuevo método no produce inmediatamente buenos resultados, la tendencia es volver a hacer algo cómodo incluso cuando no está funcionando. Pregúntele a cualquier golfista.
Para obtener mejores resultados, aquellos que no estén familiarizados con el DMA deben insistir en recibir datos que sean relevantes para la forma en que se utilizará la pieza que están desarrollando, y deben obtener una tabla de valores que luego puedan trazar para que puedan sentirse cómodos con lo que los datos les están diciendo.
A pesar de que tener una gráfica de módulo frente a temperatura ya es un gran paso más allá de la HDT, como muestra la fig. 1, el DMA proporciona mucho más. En nuestra próxima y última entrega de esta serie daremos una breve introducción a las características adicionales que proporciona un DMA.
Acerca del autor
Michael Sepe
Consultor independiente sobre materiales y procesamiento, a nivel global, cuya compañía, Michael P. Sepe, LLC, tiene su sede en Sedona, Arizona. Tiene más de 40 años de experiencia en la industria del plástico y asesora sus clientes en selección de materiales, diseño para manufactura, optimización de procesos, solución de problemas y análisis de fallos. Contacto: (928) 203-0408 • mike@thematerialanalyst.com
CONTENIDO RELACIONADO
-
Elastómeros termoplásticos (TPE): propiedades y aplicaciones
Descubra cómo los elastómeros termoplásticos revolucionan la industria gracias a su flexibilidad, facilidad de procesamiento y potencial de reciclaje.
-
El trabajo más importante de un procesador, parte 7: factores que influyen en la cristalinidad
Además de la velocidad de enfriamiento, hay varios problemas relacionados con el proceso que influyen en la cristalinidad. Examinemos algunos de ellos.
-
El trabajo más importante de un procesador, parte 5: polímeros semicristalinos
Utilizar una temperatura de molde por encima de la Tg de un polímero garantiza un grado de cristalinidad lo suficientemente alto para proporcionar una estabilidad dimensional, incluso si la pieza debe utilizarse a temperaturas elevadas. Pero el POM es una excepción. ¿Por qué?



.jpg;width=70;height=70;mode=crop)









