Extrusión: Problemas con los datos a una sola temperatura, parte 2

En la columna del mes pasado comenzamos una discusión sobre los problemas asociados con el tratamiento tradicional de las propiedades de los materiales plásticos en términos de datos con una sola temperatura. En artículos siguientes vamos a profundizar más en este tema y vamos a proporcionar algunas alternativas que están dentro de la capacidad de la tecnología actual. Este mes abordamos las propiedades que se derivan de ensayos de tracción. La mayoría de hojas de datos proporcionarán uno o dos puntos de datos sobre propiedades de tracción o tensión.

Una caracterización relativamente exhaustiva dará lugar a valores de esfuerzo de tracción y de elongación a la fluencia y a la ruptura. Para materiales dúctiles como el polietileno o el policarbonato, los límites de fluencia y de ruptura están relativamente alejados en la escala de elongación; por lo tanto, es útil conocer las propiedades en ambos puntos. Para materiales muy rígidos y frágiles los límites de fluencia y ruptura pueden ser esencialmente los mismos; por lo tanto, apuntar uno de estos puntos de referencia es suficiente. Por supuesto, la gran mayoría de las hojas de datos que ofrecen estos puntos de datos hacen las mediciones sólo a temperatura ambiente.

Es importante recordar que aunque una hoja de datos da valores de esfuerzo y elongación en la fluencia y la ruptura, simplemente representan puntos en una curva, así como el módulo que hablamos el mes pasado es un punto de una curva. Para entender verdaderamente el comportamiento de un material, necesitamos la curva. Las curvas de esfuerzo y deformación se pueden generar en una variedad de formas, pero los resultados de resistencia a la tracción son probablemente los más útiles porque dan como resultado un punto de falla bien definido. Las pruebas de resistencia a la flexión por lo general se detienen cuando la muestra alcanza una deformación de 5% y para muchos materiales no es probable que se presente una falla total en flexión o compresión. Por lo tanto, la curva a la tracción esfuerzo-deformación es una de las piezas más útiles de información que podemos tener al intentar comprender el espectro completo del comportamiento mecánico de un material.

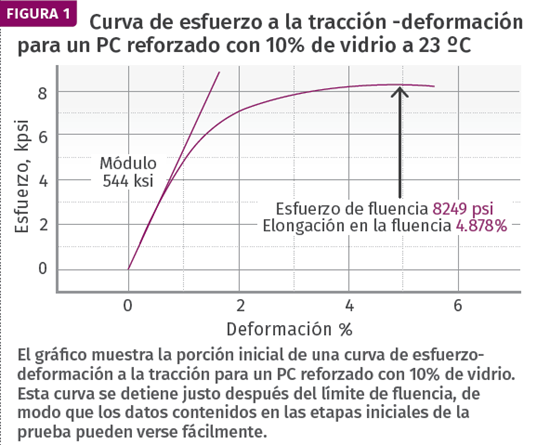
La figura 1 muestra la parte inicial de una curva de esfuerzo-deformación a la tracción de un policarbonato reforzado con fibra de vidrio al 10%. Esta curva se detiene justo después del límite de fluencia de modo que los datos contenidos en las etapas iniciales de la prueba pueden verse fácilmente. La elongación a la rotura real se produce aproximadamente a 35% de elongación y a un esfuerzo de 6500 psi. El límite de fluencia es de interés porque representa el punto donde no se requiere más aumento en el esfuerzo para producir un aumento en la deformación. Por lo tanto, no deberíamos esperar poder usar el material por encima del esfuerzo de fluencia, incluso durante un período muy corto. Y aunque mantenemos el marco de tiempo muy corto, podemos estar muy seguros de que cualquiera que sea la elongación el resultado no será recuperable.

La figura 1 contiene los puntos clave que habitualmente se obtienen de la hoja de datos; el esfuerzo y elongación de fluencia, así como el módulo. Como dijimos el mes pasado, el módulo sólo se aplica a la región de la curva de esfuerzo-deformación donde la gráfica es lineal, cuando el esfuerzo y la deformación están en proporción. Más allá del límite proporcional, la gráfica cambia de una línea a una curva y entramos en la región de deformación plástica. La aplicación sostenida de esfuerzos por encima de este punto también dará lugar a una deformación no recuperable.

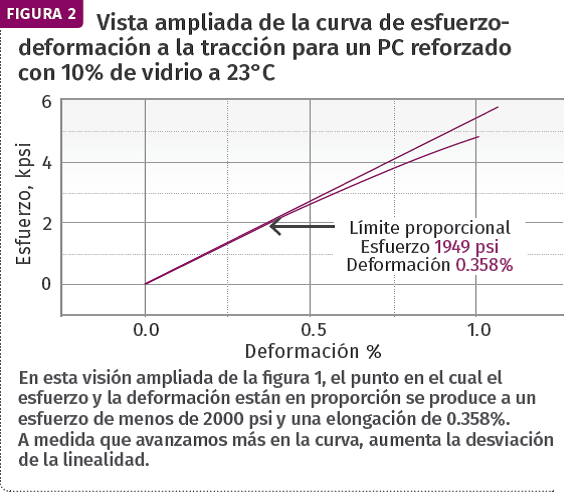
Es difícil decir a partir de la figura 1 exactamente donde cae este límite proporcional, pero la vista ampliada en la figura 2 muestra que se encuentra en un esfuerzo menor de 2000 psi y una elongación de 0.358%. Esto es menos del 25% del esfuerzo en el límite de fluencia y menos de 8% de la elongación en la fluencia. A medida que avanzamos más en la curva, aumenta la desviación de linealidad. En otras palabras, para cada aumento incremental en el esfuerzo, el aumento de la elongación asociada se hace más grande. Por ejemplo, si aumentamos el esfuerzo de 1000 a 2000 psi, la elongación instantánea aumenta en 0,19%. Sin embargo, cuando el esfuerzo aumenta de 6000 a 7000 psi, este mismo cambio incremental produce un aumento en la deformación de 0,57%, tres veces mayor.

Esto es importante porque ilustra cómo el aumento progresivo de un comportamiento no lineal de materiales plásticos influye en su desempeño. Esto se hace aún más crítico cuando el tiempo se agrega a la ecuación. La carga constante (creep) o carga cíclica (fatiga) reduce el esfuerzo máximo de trabajo que puede soportar un material plástico como una función del tiempo. Cuanto más tiempo necesite funcionar el producto, menos esfuerzo podrá soportar. Esto explica por qué los ingenieros que están acostumbrados a trabajar con metales se sorprenden de que los materiales plásticos no pueden funcionar tan cerca de su límite de fluencia como los metales. También explica por qué las personas que llevan a cabo análisis de elementos finitos (FEA) pueden tener tantos problemas cuando se realiza un análisis lineal en materiales plásticos. La linealidad se aplica sólo para un segmento muy pequeño de la curva de esfuerzo-deformación.

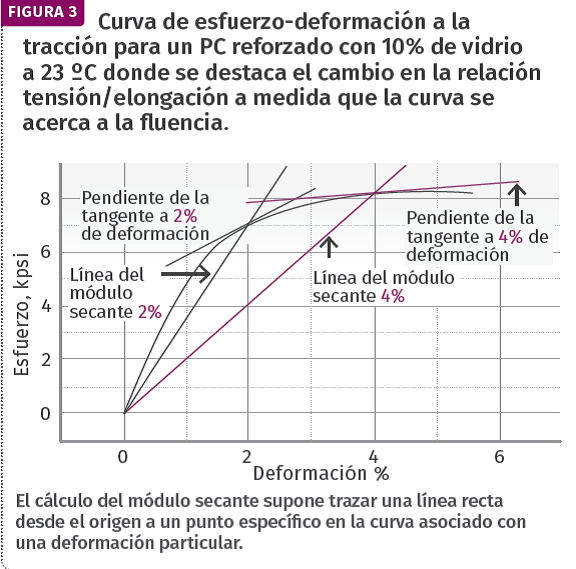
A menudo se toman atajos mediante el cálculo de un módulo secante, como se muestra en la figura 3. Se trata de trazar una línea recta desde el origen hasta un punto específico en la curva asociado con una elongación particular. Generalmente esto se hace en el punto de 1% o 2%. Ya que los materiales plásticos son no-lineales en estas elongaciones, la línea recta que define el módulo secante representa una reducción de la propiedad asociada a la porción lineal de la gráfica de esfuerzo-deformación. En el caso de este policarbonato, la pendiente de la línea que une el origen a la coordenada en una deformación del 2% da un módulo de 350 kpsi, significativamente menor que el de 544kpsi  que se muestra en la figura 1. Si se realiza esta misma operación hasta el punto del 4% de deformación, el módulo asociado a esta línea es sólo de 210 kpsi.

Pero las preocupaciones por las propiedades de carga a largo plazo son aún mayores cuando entendemos que la velocidad a la que ocurre un aumento progresivo de la deformación bajo la influencia de un esfuerzo particular está gobernada más exactamente por la pendiente de la línea tangente dibujada para la curva esfuerzo-deformación en el punto de interés. Si consideramos las cosas de esta manera, podemos ver que la pendiente de la línea tangente a la curva en una deformación del 2% es sólo 120 kpsi y en deformación de 4% es sólo 19 kpsi. La velocidad del aumento de la deformación con carga prolongada asociada a los esfuerzos en la región no lineal de la curva se verá reflejada en esta pendiente, de modo que a medida que la elongación inicial asociada a un caso de carga particular aumenta, el tiempo que el material puede funcionar antes de fallar se reduce significativamente.

Así que la pregunta es: ¿Cómo van a tomar decisiones inteligentes los ingenieros sobre la idoneidad de un material bajo carga si no tienen acceso a la curva real esfuerzo-deformación? Es bueno saber el límite de fluencia porque representa un límite de rendimiento superior para el comportamiento a muy corto plazo. Pero para considerar aplicaciones a largo plazo necesitamos saber cómo llegamos al límite de fluencia. Es posible trazar las curvas de varias formas diferentes donde todas empiecen en cero y terminen en aproximadamente el mismo límite de fluencia. Estos caminos diferentes señalan que el rendimiento de los materiales será diferente. Y aún no hemos empezado a considerar los efectos de la temperatura en las formas de estas curvas. Para esto tendremos que esperar hasta el siguiente artículo.

Lea a continuación Parte 3: límite de fluencia.